The order of a Tree
Problem Description
As we know,the shape of a binary search tree is greatly related to the order of keys we insert. To be precisely: 1. insert a key k to a empty tree, then the tree become a tree with only one node; 2. insert a key k to a nonempty tree, if k is less than the root ,insert it to the left sub-tree;else insert k to the right sub-tree. We call the order of keys we insert “the order of a tree”,your task is,given a oder of a tree, find the order of a tree with the least lexicographic order that generate the same tree.Two trees are the same if and only if they have the same shape.
Input
There are multiple test cases in an input file. The first line of each testcase is an integer n(n <= 100,000),represent the number of nodes.The second line has n intergers,k1 to kn,represent the order of a tree.To make if more simple, k1 to kn is a sequence of 1 to n.
Output
One line with n intergers, which are the order of a tree that generate the same tree with the least lexicographic.
Sample Input
41 3 4 2
Sample Output
1 3 2 4
解释:
给定一个序列,构成一颗二叉排序树,然后要求计算出一个新的序列,还是原先序列的数,所构造的二叉排序树也一样,并且字典序还是最小的。
例如:4 6 5 7 2 1 3
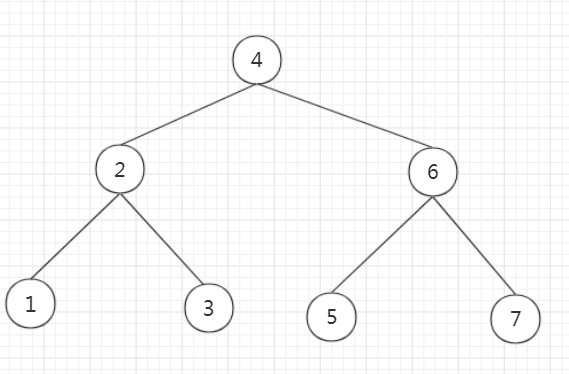
那么要求最小的字典序。对于二叉排序树,根节点是最先构造好的,并且对于左孩子和有孩子的添加新元素是不会有影响的,也就是说当一个新的数插入的时候,要么在左孩子中,要么在右孩子中,并且要求一个新的序列并且构造的二叉排序树还是一样的,那就是先给出左边的孩子,再给右边的孩子。或者先给右边的孩子,再给左边的孩子。对于要求字典序最小,就先给左孩子,但是根节点要先给出来,不然二叉排序数就会乱。所以,就是一个先序遍历的过程。这个二叉排序树的答案就是 4 2 1 3 6 5 7. 同时我们再看看后序:1 3 2 5 7 6 4, 树的结构变了,中序:1 2 3 4 5 6 7,输的结构也变了。层次遍历:4 2 6 1 3 5 7,树的结构没有变,但是不如先序便来的字典序小。一开始我就是输出层次遍历的结果,然后发现不对。啦啦啦啦,其实是我一开始就没有看懂这些英语,我以为是换一个不一样的序列,然后二叉排序树一样就可以了。之后才发现least lexicographic。


1 #include2 3 using namespace std; 4 5 const int N = 101000; 6 7 struct point{ 8 int value; 9 int rx, lx;10 } res[N];11 12 int t = 0, n;13 void Out(int i) {14 15 if (!res[i].value) return ;16 printf("%d%c", res[i].value, t++ == n-1 ? '\n' : ' ');17 Out(res[i].lx);18 Out(res[i].rx);19 20 }21 22 int main () {23 24 while (~scanf("%d", &n)) {25 memset(res, 0, sizeof(res));26 for (int i = 1; i <= n; i++) {27 int x, tx = 1;28 scanf("%d", &x);29 if (i == 1) {30 res[1].value = x;31 } else {32 while (true) {33 if (x < res[tx].value) {34 if (!res[tx].lx) {35 res[tx].lx = i;36 res[i].value = x;37 break;38 } else tx = res[tx].lx;39 } else {40 if (!res[tx].rx) {41 res[tx].rx = i;42 res[i].value = x;43 break;44 } else tx = res[tx].rx;45 }46 }47 }48 }49 50 // for (int i = 0; i <= n; i++) {51 // printf("%d %d %d %d\n", i, res[i].value, res[i].lx, res[i].rx);52 // }53 Out(1);54 55 }56 return 0;57 }